Project 4: Scheme Interpreter
Eval calls apply,
which just calls eval again!
When does it all end?
Introduction
Note: If you're interested in an alternate version of this project that gives you considerably less scaffolding and guidance, you can try the Scheme Challenge Version! For grading purposes, completing either version of the project (this version or the Challenge version) will be equivalent.
Important submission note: For full credit,
- Submit with Part 1 complete by Tuesday, April 12 (worth 1 pt).
- Submit with Parts 2 & 3 (including passing all tests provided in
tests.scm) complete by Tuesday, April 19 (worth 1 pt).- Submit with all phases complete by Tuesday, April 26.
Try to attempt the problems in order, as some later problems will depend on earlier problems in their implementation and therefore also when running
oktests.The entire project can be completed with a partner.
You can get 1 bonus point by submitting the entire project by Monday, April 25.
In this project, you will develop an interpreter for a subset of the Scheme language. As you proceed, think about the issues that arise in the design of a programming language; many quirks of languages are byproducts of implementation decisions in interpreters and compilers. The subset of the language used in this project is described in the functional programming section of Composing Programs, as well as this language specification and built-in procedure reference for the CS 61A subset of Scheme that you'll be building in this project.
Watch (or attend) the lectures on Calculator and Interpreters for an overview of the project.
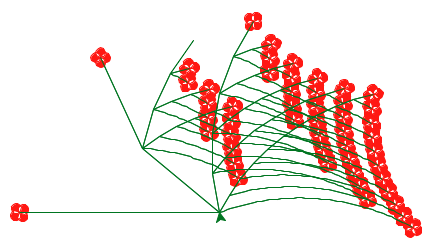
In addition, there will be a completely optional open-ended art contest (released separately) that challenges you to produce recursive images in only a few lines of Scheme. As an example, the picture above abstractly depicts all the ways of making change for $0.50 using U.S. currency. All flowers appear at the end of a branch with length 50. Small angles in a branch indicate an additional coin, while large angles indicate a new currency denomination. In the contest, you too will have the chance to unleash your inner recursive artist.
Download starter files
You can download all of the project code as a zip archive.
Files you will edit:
scheme_eval_apply.py: the recursive evaluator for Scheme expressionsscheme_forms.py: evaluation for special formsscheme_classes.py: classes that describe Scheme expressionsquestions.scm: contains skeleton code for Part 3
The rest of the files in the project:
scheme.py: the interpreter REPLpair.py: defines thePairclass and thenilobjectscheme_builtins.py: built-in Scheme proceduresscheme_reader.py: the reader for Scheme input (this file is obfuscated so that you can implement it in lab)scheme_tokens.py: the tokenizer for Scheme inputscheme_utils.py: functions for inspecting Scheme expressionsucb.py: utility functions for use in 61A projectstests.scm: a collection of test cases written in Schemeok: the autogradertests: a directory of tests used byokmytests.rst: a file where you can add your own tests
Logistics
The project is worth points.
28 points are for correctness,
which is including 1 point for passing tests.scm.
1 point is for submitting Part 1 by the first checkpoint date,
and 1 point is for submitting Parts 2 & 3 by the second checkpoint date.
Additionally, there are some extra credit point opportunities. You can get 1 EC point for submitting the entire project by Monday, April 25, and 2 EC points for submitting the extra credit problem.
Important: In order to receive all of the possible extra credit points for Scheme, your implementation of the entire project, including the EC problem, must be submitted by the early submission deadline.
You will turn in the following files:
scheme_eval_apply.pyscheme_forms.pyscheme_classes.pyquestions.scm
You do not need to modify or turn in any other files to complete the project. To submit the project, run the following command:
python3 ok --submitYou will be able to view your submissions on the Ok dashboard.
For the functions that we ask you to complete, there may be some initial code that we provide. If you would rather not use that code, feel free to delete it and start from scratch. You may also add new function definitions as you see fit.
However, please do not modify any other functions or edit any files not listed above. Doing so may result in your code failing our autograder tests. Also, please do not change any function signatures (names, argument order, or number of arguments).
Throughout this project, you should be testing the correctness of your code. It is good practice to test often, so that it is easy to isolate any problems. However, you should not be testing too often, to allow yourself time to think through problems.
We have provided an autograder called ok to help you
with testing your code and tracking your progress. The first time you run the
autograder, you will be asked to log in with your Ok account using your web
browser. Please do so. Each time you run ok, it will back up
your work and progress on our servers.
The primary purpose of ok is to test your implementations.
We recommend that you submit after you finish each problem. Only your last submission will be graded. It is also useful for us to have more backups of your code in case you run into a submission issue. If you forget to submit, your last backup will be automatically converted to a submission.
If you do not want us to record a backup of your work or information about your progress, you can run
python3 ok --localWith this option, no information will be sent to our course servers. If you want to test your code interactively, you can run
python3 ok -q [question number] -iwith the appropriate question number (e.g.
01) inserted.
This will run the tests for that question until the first one you failed,
then give you a chance to test the functions you wrote interactively.
You can also use the debugging print feature in OK by writing
print("DEBUG:", x)
which will produce an output in your terminal without causing OK tests to fail
with extra output.
Interpreter details
Scheme features
Read-Eval-Print. The interpreter reads Scheme expressions, evaluates them, and displays the results.
scm> 2
2
scm> (+ 2 3)
5
scm> ((lambda (x) (* x x)) 5)
25The starter code for your Scheme interpreter can successfully evaluate the first expression above, since it consists of a single number. The second (a call to a built-in procedure) and the third (a computation of 5 squared) will not work just yet.
Load. You can load a file by passing in a symbol for the file name.
For example, to load tests.scm, evaluate the following call expression.
scm> (load 'tests)Symbols. Various dialects of Scheme are more or less permissive about identifiers (which serve as symbols and variable names).
Our rule is that:
An identifier is a sequence of letters (a-z and A-Z), digits, and characters in
!$%&*/:<=>?@^_~-+.that do not form a valid integer or floating-point numeral and are not existing special form shorthands.
Our version of Scheme is case-insensitive: two identifiers are considered identical if they differ only in the capitalization of letters. They are internally represented and printed in lower case:
scm> 'Hello
helloTurtle Graphics. In addition to standard Scheme procedures, we include
procedure calls to the Python turtle package. This will come in handy
for the contest. You do not have to install this package in order to participate.
If you're curious, you can read the turtle module documentation online.
Running the interpreter
To start an interactive Scheme interpreter session, type:
python3 scheme.pyCurrently, your Scheme interpreter can handle a few simple expressions, such as:
scm> 1
1
scm> 42
42
scm> true
#tTo exit the Scheme interpreter, press Ctrl-d or evaluate the exit procedure
(after completing problems 3 and 4):
scm> (exit)You can use your Scheme interpreter to evaluate the expressions in an input file
by passing the file name as a command-line argument to scheme.py:
python3 scheme.py tests.scmThe tests.scm file contains a long list of sample Scheme expressions and
their expected values. Many of these examples are from Chapters 1 and 2 of
Structure and Interpretation of Computer Programs, the textbook from
which Composing Programs is adapted.
Part 1: The Evaluator
In Part 1, you will develop the following features of the interpreter:
- Symbol evaluation
- Calling built-in procedures
- Definitions
In the starter implementation given to you, the evaluator can only evaluate
self-evaluating expressions: numbers, booleans, and nil.
First, read the relevant code. In the "Eval/Apply" section of
scheme_eval_apply.py:
scheme_evalevaluates a Scheme expression in the given environment. This function is nearly complete but is missing the logic for call expressions.- When evaluating a special form,
scheme_evalredirects evaluation to an appropriatedo_?_formfunction found inscheme_forms.py scheme_applyapplies a procedure to some arguments. This function has cases for the various types of procedures (builtin procedures, user-defined procedures, and so forth) that you will implement.
In the "Environments" and "Procedures" section of scheme_classes.py:
- The
Frameclass implements an environment frame. - The
LambdaProcedureclass (in the "Procedures" section) represents user-defined procedures.
These are all of the essential components of the interpreter. scheme_forms.py defines special forms,
scheme_builtins.py defines the various functions built into the standard library, and scheme.py defines input/output behavior.
Use Ok to test your understanding:
python3 ok -q eval_apply -uProblem 1 (1 pt)
Implement the define and lookup methods of the Frame class, in scheme_classes.py.
Each Frame object has the following instance attributes:
bindingsis a dictionary representing the bindings in the frame. It maps Scheme symbols (represented as Python strings) to Scheme values.parentis the parentFrameinstance. The parent of the Global Frame isNone.
definetakes a symbol (represented by a Python string) and a value. It binds the symbol to the value in theFrameinstance.lookuptakes a symbol and returns the value bound to that symbol in the first frame of the environment in which the symbol is bound. The environment for aFrameinstance consists of that frame, its parent frame, and all its ancestor frames, including the Global Frame. This is explained below:- If the symbol is bound in the current frame, return its value.
- If the symbol is not bound in the current frame, and the frame has a parent frame, continue lookup in the parent frame.
- If the symbol is not found in the current frame and there is no parent frame,
raise a
SchemeError.
Use Ok to unlock and test your code:
python3 ok -q 01 -u
python3 ok -q 01After you complete this problem, you can start your Scheme interpreter
(with python3 scheme.py). You should be able to look up built-in
procedure names:
scm> +
#[+]
scm> odd?
#[odd?]However, your Scheme interpreter will still not be able to call these procedures. Let's fix that.
Remember, at this point you can only exit the interpreter by pressing Ctrl-d.
Problem 2 (2 pt)
To be able to call built-in procedures, such as +, you need to complete the
BuiltinProcedure case within the scheme_apply function in
scheme_eval_apply.py. Built-in procedures are applied by calling a
corresponding Python function that implements the procedure.
To see a list of all Scheme built-in procedures used in the project, look in the
scheme_builtins.pyfile. Any function decorated with@builtinwill be added to the globally-definedBUILTINSlist.
A BuiltinProcedure has two instance attributes:
py_func: the Python function that implements the built-in Scheme procedure.expect_env: a Boolean flag that indicates whether or not this built-in procedure will expect the current environment to be passed in as the last argument. The environment is required, for instance, to implement the built-inevalprocedure.
scheme_apply takes the procedure object, a list of argument values, and
the current environment. args is a Scheme list represented as a
Pair object or nil. Your implementation should do the following:
- Convert the Scheme list to a Python list of arguments. Hint:
argsis a Pair, which has a.firstand.restsimilar to a Linked List. Think about how you would put the values of a Linked List into a list. - If
procedure.expect_envisTrue, then add the current environmentenvas the last argument to this Python list. - Call
procedure.py_funcon all of those arguments using*argsnotation (f(1, 2, 3)is equivalent tof(*[1, 2, 3])). - If calling the function results in a
TypeErrorexception being raised, then the wrong number of arguments were passed. Use atry/exceptblock to intercept the exception and raise aSchemeErrorwith the message'incorrect number of arguments'. - Otherwise,
scheme_applyshould return the value obtained by callingprocedure.py_func
Use Ok to unlock and test your code:
python3 ok -q 02 -u
python3 ok -q 02👩🏽💻👨🏿💻 Pair programming? Remember to alternate between driver and navigator roles. The driver controls the keyboard; the navigator watches, asks questions, and suggests ideas.
Problem 3 (2 pt)
The scheme_eval function (in scheme_eval_apply.py) evaluates a Scheme
expression (represented as a Pair) in a given environment. The provided code
already looks up names in the current environment, returns self-evaluating
expressions (such as numbers) and evaluates special forms.
Implement the missing part of scheme_eval, which evaluates a call expression.
To evaluate a call expression:
- Evaluate the operator (which should evaluate to an instance of
Procedure) - Evaluate all of the operands
- Apply the procedure on the evaluated operands by calling
scheme_apply, then return the result
You'll have to recursively call scheme_eval in the first two steps. Here are
some other functions/methods you should use:
- The
mapmethod ofPairreturns a new Scheme list constructed by applying a one-argument function to every item in a Scheme list. - The
scheme_applyfunction applies a Scheme procedure to arguments represented as a Scheme list (aPairinstance).
Important: do not mutate the passed-in expr. That would change a program as
it's being evaluated, creating strange and incorrect effects.
Use Ok to unlock and test your code:
python3 ok -q 03 -u
python3 ok -q 03Some of these tests call a primitive (built-in) procedure called
print-then-return. This procedure doesn't exist in Scheme, but was added to this project just to test this question.print-then-returntakes two arguments. It prints out its first argument and returns the second. You can find this function at the bottom ofscheme_builtins.py
Your interpreter should now be able to evaluate built-in procedure calls, giving
you the functionality of the Calculator language and more. Run python3
scheme.py, and you can now add and multiply!
scm> (+ 1 2)
3
scm> (* 3 4 (- 5 2) 1)
36
scm> (odd? 31)
#tProblem 4 (2 pt)
The define special form (spec) in Scheme can be used either to assign a name to the
value of a given expression or to create a procedure and bind it to a name:
scm> (define a (+ 2 3)) ; Binds the name a to the value of (+ 2 3)
a
scm> (define (foo x) x) ; Creates a procedure and binds it to the name foo
fooThe type of the first operand tells us what is being defined:
- If it is a symbol, e.g.
a, then the expression is defining a name - If it is a list, e.g.
(foo x), then the expression is defining a procedure.
The do_define_form function in scheme_forms.py evaluates (define ...)
expressions. There are two missing parts in this function. For this problem,
implement just the first part, which evaluates the second operand to obtain
a value and binds the first operand, a symbol, to that value. Then,
do_define_form returns the symbol that was bound.
Use Ok to unlock and test your code:
python3 ok -q 04 -u
python3 ok -q 04You should now be able to give names to values and evaluate the resulting
symbols. For example, here are some test cases from the ok tests for this
question.
scm> (define x 15)
x
scm> (define y (* 2 x))
y
scm> y
30
scm> (+ y (* y 2) 1)
91
scm> (define x 20)
x
scm> x
20For this test, the goal is to highlight whether the operator is evaluated multiple times before raising an error. The expected, and intended behavior is for the operator to be evaluated only a single time before raising the error.
(define x 0)
; expect x
((define x (+ x 1)) 2)
; expect Error
x
; expect 1We expect an error to be raised here since the operator does not evaluate to a
procedure. However, if the operator is evaluated multiple times before
raising an error, x will be bound to 2 instead of 1, causing the test to fail.
Therefore, if your interpreter fails this test, you'll want to make sure you
only evaluate the operator once in scheme_eval.
Problem 5 (1 pt)
In Scheme, you can quote expressions in two ways: with the quote special form
(spec) or with the symbol '. The reader converts '... into
(quote ...), so that your interpreter only needs to evaluate the (quote ...)
syntax. The quote special form returns its operand expression without
evaluating it:
scm> (quote hello)
hello
scm> '(cons 1 2) ; Equivalent to (quote (cons 1 2))
(cons 1 2)Implement the do_quote_form function in scheme_forms.py so that it simply
returns the unevaluated operand of the (quote ...) expression.
Use Ok to unlock and test your code:
python3 ok -q 05 -u
python3 ok -q 05After completing this function, you should be able to evaluate quoted expressions. Try out some of the following in your interpreter!
scm> (quote a)
a
scm> (quote (1 2))
(1 2)
scm> (quote (1 (2 three (4 5))))
(1 (2 three (4 5)))
scm> (car (quote (a b)))
a
scm> 'hello
hello
scm> '(1 2)
(1 2)
scm> '(1 (2 three (4 5)))
(1 (2 three (4 5)))
scm> (car '(a b))
a
scm> (eval (cons 'car '('(1 2))))
1
scm> (eval (define tau 6.28))
6.28
scm> (eval 'tau)
6.28
scm> tau
6.28Once you have completed Problem 5, make sure you submit using OK to receive full credit for the first checkpoint.
python3 ok --submitIf you'd like to check your score so far, use the following command:
python3 ok --score
Part 2: Procedures
In Part 2, you will add the ability to create and call user-defined procedures. You will add the following features to the interpreter:
- Lambda procedures, using the
(lambda ...)special form - Named lambda procedures, using the
(define (...) ...)special form - Mu procedures, with dynamic scope
User-Defined Procedures
User-defined lambda procedures are represented as instances of the LambdaProcedure
class. A LambdaProcedure instance has three instance attributes:
formalsis a Scheme list of the formal parameters (symbols) that name the arguments of the procedure.bodyis a Scheme list of expressions; the body of the procedure.envis the environment in which the procedure was defined.
Problem 6 (1 pt)
Change the eval_all function in scheme_eval_apply.py (which is called from
do_begin_form in scheme_forms.py) to complete the implementation of the
begin special form (spec).
A begin expression is evaluated by evaluating all sub-expressions in order.
The value of the begin expression is the value of the final sub-expression.
To complete the implementation of begin, eval_all will take in expressions
(a Scheme list of expressions) and env (a Frame representing the current
environment), evaluate all the expressions in expressions, and return the
value of the last expression in expressions.
scm> (begin (+ 2 3) (+ 5 6))
11
scm> (define x (begin (display 3) (newline) (+ 2 3)))
3
x
scm> (+ x 3)
8
scm> (begin (print 3) '(+ 2 3))
3
(+ 2 3)If eval_all is passed an empty list of expressions (nil), then it should
return the Python value None, which represents the Scheme value undefined.
Use Ok to unlock and test your code:
python3 ok -q 06 -u
python3 ok -q 06👩🏽💻👨🏿💻 Pair programming? This would be a good time to switch roles. Switching roles makes sure that you both benefit from the learning experience of being in each role.
Problem 7 (2 pt)
Implement the do_lambda_form function (spec) in
scheme_forms.py, which creates and returns a LambdaProcedure instance.
While you cannot call a user-defined procedure yet, you can verify that you
have created the procedure correctly by typing a lambda expression into the
interpreter prompt:
scm> (lambda (x y) (+ x y))
(lambda (x y) (+ x y))In Scheme, it is legal to place more than one expression in the body of a
procedure. (There must be at least one expression.) The body attribute of a
LambdaProcedure instance is therefore a Scheme list of body expressions. The
formals attribute of a LambdaProcedure instance should be a properly nested
Pair expression. Like a begin special form, evaluating the body of a
procedure evaluates all body expressions in order. The return value of a
procedure is the value of its last body expression.
Use Ok to unlock and test your code:
python3 ok -q 07 -u
python3 ok -q 07Problem 8 (2 pt)
Implement the make_child_frame method of the Frame class
(in scheme_classes.py), which will be used to create new frames when calling
user-defined procedures. This method takes in two arguments: formals, which is
a Scheme list of symbols, and vals, which is a Scheme list of values. It
should return a new child frame, binding the formal parameters to the values.
To do this:
- If the number of argument values does not match with the number of formal parameters, raise a
SchemeError. - Create a new
Frameinstance, the parent of which isself. - Bind each formal parameter to its corresponding argument value in the newly
created frame. The first symbol in
formalsshould be bound to the first value invals, and so on. - Return the new frame.
Hint: The
definemethod of aFrameinstance creates a binding in that frame.
Use Ok to unlock and test your code:
python3 ok -q 08 -u
python3 ok -q 08Problem 9 (2 pt)
Implement the LambdaProcedure case in the scheme_apply function
(in scheme_eval_apply.py).
You should first create a new Frame instance using the make_child_frame
method of the appropriate parent frame, binding formal parameters to argument
values. Then, evaluate each of the expressions of the body of the procedure
using eval_all within this new frame.
Your new frame should be a child of the frame in which the lambda is defined.
Note that the env provided as an argument to scheme_apply is instead the
frame in which the procedure is called.
See User-Defined Procedures to remind yourself
of the attributes of LambdaProcedure.
Use Ok to unlock and test your code:
python3 ok -q 09 -u
python3 ok -q 09Problem 10 (1 pt)
Currently, your Scheme interpreter is able to bind symbols to user-defined procedures in the following manner:
scm> (define f (lambda (x) (* x 2)))
fHowever, we'd like to be able to use the shorthand form of defining named procedures:
scm> (define (f x) (* x 2))
fModify the do_define_form function in scheme_forms.py so that it correctly handles
define (...) ...) expressions (spec).
Make sure that it can handle multi-expression bodies. For example,
scm> (define (g y) (print y) (+ y 1))
g
scm> (g 3)
3
4Your implementation should do the following:
- Using the given variables
signatureandexpressions, find the defined function's name (symbol), formals, and body. - Create a
LambdaProcedureinstance using the formals and body. Hint: You can use what you've done in Problem 8 and calldo_lambda_formon the appropriate arguments. - Bind the symbol to this new
LambdaProcedureinstance.
Use Ok to unlock and test your code:
python3 ok -q 10 -u
python3 ok -q 10Problem 11 (1 pt)
All of the Scheme procedures we've seen so far use lexical scoping: the parent of the new call frame is the environment in which the procedure was defined. Another type of scoping, which is not standard in Scheme but appears in other variants of Lisp, is called dynamic scoping: the parent of the new call frame is the environment in which the call expression was evaluated. With dynamic scoping, calling the same procedure with the same arguments from different parts of your code can create different behavior (due to different parent frames).
The mu special form (spec; invented for this project) evaluates
to a dynamically scoped procedure.
scm> (define f (mu () (* a b)))
f
scm> (define g (lambda () (define a 4) (define b 5) (f)))
g
scm> (g)
20Above, the procedure f does not have a or b as arguments; however, because
f gets called within the procedure g, it has access to the a and b
defined in g's frame.
Implement do_mu_form in scheme_forms.py to evaluate the mu special form. A
mu expression evaluates to a MuProcedure. Most of the MuProcedure class
(defined in scheme_classes.py) has been provided for you.
In addition to implementing do_mu_form, complete the MuProcedure case
within the scheme_apply function (in scheme_eval_apply.py) so that when a
mu procedure is called, its body is evaluated in the correct environment. When
a MuProcedure is called, the parent of the new call frame is the environment
in which that call expression was evaluated. As a result, a MuProcedure
does not need to store an environment as an instance attribute.
Use Ok to unlock and test your code:
python3 ok -q 11 -u
python3 ok -q 11At this point in the project, your Scheme interpreter should support the following features:
- Creating procedures using
lambdaandmuexpressions, - Defining named procedures using
defineexpressions, and - Calling user-defined procedures.
Part 3: Special Forms
This section will be completed in scheme_forms.py.
Logical special forms include if, and, or, and cond. These expressions
are special because not all of their sub-expressions may be evaluated.
In Scheme, only #f is a false value. All other values
(including 0 and nil) are true values. You can test whether a value is a
true or false value using the provided Python functions is_scheme_true and
is_scheme_false, defined in scheme_utils.py.
Scheme traditionally uses
#fto indicate the false Boolean value. In our interpreter, that is equivalent tofalseorFalse. Similarly,true,True, and#tare all equivalent. However, when unlocking tests, use#tand#f.
To get you started, we've provided an implementation of the if special form in
the do_if_form function. Make sure you understand that implementation before
starting the following questions.
Problem 12 (2 pt)
Implement do_and_form and do_or_form so that and and or expressions
(spec) are evaluated correctly.
The logical forms and and or are short-circuiting. For and, your
interpreter should evaluate each sub-expression from left to right, and if any
of these is a false value, return that value. Otherwise,
return the value of the last sub-expression. If there are no
sub-expressions in an and expression, it evaluates to #t.
scm> (and)
#t
scm> (and 4 5 6) ; all operands are true values
6
scm> (and 4 5 (+ 3 3))
6
scm> (and #t #f 42 (/ 1 0)) ; short-circuiting behavior of and
#fFor the
andandorforms, remember to use our internal Python representations of#tand#f. See internal representations from Lab 11.
For or, evaluate each sub-expression from left to right. If any
sub-expression evaluates to a true value, return that value. Otherwise, return
the value of the last sub-expression.
If there are no sub-expressions in an or expression,
it evaluates to #f.
scm> (or)
#f
scm> (or 5 2 1) ; 5 is a true value
5
scm> (or #f (- 1 1) 1) ; 0 is a true value in Scheme
0
scm> (or 4 #t (/ 1 0)) ; short-circuiting behavior of or
4Important: Use the provided Python functions is_scheme_true and
is_scheme_false from scheme_utils.py to test boolean values.
Use Ok to unlock and test your code:
python3 ok -q 12 -u
python3 ok -q 12Problem 13 (2 pt)
Fill in the missing parts of do_cond_form so that it correctly implements
cond (spec), returning the value of the first result
sub-expression corresponding to a true predicate, or the result sub-expression
corresponding to else.
Some special cases:
- When the true predicate does not have a corresponding result sub-expression, return the predicate value.
- When a result sub-expression of a
condcase has multiple expressions, evaluate them all and return the value of the last expression. (Hint: Useeval_all.)
Your implementation should match the following examples and the additional tests
in tests.scm.
scm> (cond ((= 4 3) 'nope)
((= 4 4) 'hi)
(else 'wait))
hi
scm> (cond ((= 4 3) 'wat)
((= 4 4))
(else 'hm))
#t
scm> (cond ((= 4 4) 'here (+ 40 2))
(else 'wat 0))
42The value of a cond is undefined if there are no true predicates and no
else. In such a case, do_cond_form should return None. If there is only an
else, return its sub-expression. If it doesn't have one, return #t.
scm> (cond (False 1) (False 2))
scm> (cond (else))
#tUse Ok to unlock and test your code:
python3 ok -q 13 -u
python3 ok -q 13Problem 14 (2 pt)
The let special form (spec) binds symbols to values locally,
giving them their initial values. For example:
scm> (define x 5)
x
scm> (define y 'bye)
y
scm> (let ((x 42)
(y (* x 10))) ; this x refers to the global value of x, not 42
(list x y))
(42 50)
scm> (list x y)
(5 bye)Implement make_let_frame in scheme_forms.py, which returns a child
frame of env that binds the symbol in each element of bindings to the
value of its corresponding expression. The bindings Scheme list contains
pairs that each contain a symbol and a corresponding expression.
You may find the following functions and methods useful:
validate_form: this function can be used to validate the structure of each binding. It takes in a Scheme listexprof expressions and aminandmaxlength. Ifexpris not a list with length betweenminandmaxinclusive, it raises an error. If nomaxis passed in, the default is infinity.validate_formals: this function validates that its argument is a Scheme list of symbols for which each symbol is distinct.
Remember to refer to the spec if you don't understand any of the test cases!
Use Ok to unlock and test your code:
python3 ok -q 14 -u
python3 ok -q 14Additional Scheme Tests (1 pt)
Your final task in Part III of this project is to make sure that your scheme interpreter passes the additional suite of tests we have provided.
To run these tests (worth 1 point), run the command:
python3 ok -q tests.scmIf you have passed all of the required cases,
you should see 1/1 points
received for tests.scm when you run python ok --score.
If you are failing tests due to output from
print statements you've added in your code for debugging,
make sure to remove those as well for the tests to pass.
One you have completed Part III, make sure you submit using OK to receive full credit for the checkpoint.
python3 ok --submitIf you'd like to check your score so far, use the following command:
python3 ok --scoreThe best way to see what tests you've passed for the checkpoint is to use the score command in ok.
Congratulations! Your Scheme interpreter implementation is now complete!
Part IV: Write Some Scheme
Not only is your Scheme interpreter itself a tree-recursive program, but it is
flexible enough to evaluate other recursive programs. Implement the
following procedures in the questions.scm file.
See the built-in procedure reference for descriptions of the behavior of all built-in Scheme procedure.
As you use your interpreter, you may discover additional bugs in your interpreter implementation. Therefore, you may find it useful to test your code for these questions in the staff interpreter or the web editor and then try it in your own interpreter once you are confident your Scheme code is working. You can also use the web editor to visualize the scheme code you've written and help you debug.
Scheme Editor
As you're writing your code, you can debug using the Scheme Editor. In your
scheme folder you will find a new editor. To run this editor, run python3
editor. This should pop up a window in your browser; if it does not, please
navigate to localhost:31415 and you should see it.
Make sure to run python3 ok in a separate tab or window so that the editor
keeps running.
👩🏽💻👨🏿💻 Pair programming? Remember to alternate between driver and navigator roles. The driver controls the keyboard; the navigator watches, asks questions, and suggests ideas.
Problem 15 (2 pt)
Implement the enumerate procedure, which takes in a list of values and returns
a list of two-element lists, where the first element is the index of the value,
and the second element is the value itself.
scm> (enumerate '(3 4 5 6))
((0 3) (1 4) (2 5) (3 6))
scm> (enumerate '())
()Use Ok to test your code:
python3 ok -q 15Problem 16 (2 pt)
Implement the merge procedure, which takes in a comparator function inorder? and two lists that
are sorted, and combines the two lists into a single sorted list.
A comparator defines an ordering by comparing two values
and returning a true value if and only if the two values are ordered.
Here, sorted means sorted according to the comparator. For example:
scm> (merge < '(1 4 6) '(2 5 8))
(1 2 4 5 6 8)
scm> (merge > '(6 4 1) '(8 5 2))
(8 6 5 4 2 1)In case of a tie, you can choose to break the tie arbitrarily.
Use Ok to test your code:
python3 ok -q 16Extra Credit
During regular Office Hours and Project Parties, the staff will prioritize helping students with required questions. We will not be offering help with either extra credit problems unless the queue is empty.
Problem EC 1 (2 pt)
Complete the function optimize_tail_calls in scheme_eval_apply.py. It returns an
alternative to scheme_eval that is properly tail recursive. That is, the
interpreter will allow an unbounded number of active tail calls in constant
space. It has a third argument tail that indicates whether the expression to
be evaluated is in a tail context.
The Unevaluated class represents an expression that needs to be
evaluated in an environment. When optimized_eval receives a non-atomic
expression in a tail context, it returns an Unevaluated instance. Otherwise,
it should repeatedly call unoptimized_scheme_eval until the result is a value,
rather than an Unevaluated.
A successful implementation will require changes to several other functions,
including some functions that we provided for you. All expressions throughout
your interpreter that are in a tail context should be evaluated by calling
scheme_eval with True as the third argument (now called tail). Your goal
is to determine which expressions are in a tail context throughout your code and
change calls to scheme_eval as needed.
Tail call optimization was discussed in Lecture 29. The Unevaluated class in the Scheme interpreter is similar conceptually to the "thunk" discussed in lecture, and the missing code in optimized_eval is basically the "trampolining" technique discussed in lecture.
Once you finish, uncomment the following line in scheme_eval_apply.py to use your
implementation:
scheme_eval = optimize_tail_calls(scheme_eval)Use Ok to test your code:
python3 ok -q ECOptional Problems
Optional Problem 1 (0 pt)
In Scheme, source code is data. Every non-atomic expression is written as a Scheme list, so we can write procedures that manipulate other programs just as we write procedures that manipulate lists.
Rewriting programs can be useful: we can write an interpreter that only handles a small core of the language, and then write a procedure that converts other special forms into the core language before a program is passed to the interpreter.
For example, the let special form is equivalent to a call expression that
begins with a lambda expression. Both create a new frame extending the
current environment and evaluate a body within that new environment.
(let ((a 1) (b 2)) (+ a b))
;; Is equivalent to:
((lambda (a b) (+ a b)) 1 2)These expressions can be represented by the following diagrams:
| Let | Lambda |
|---|---|
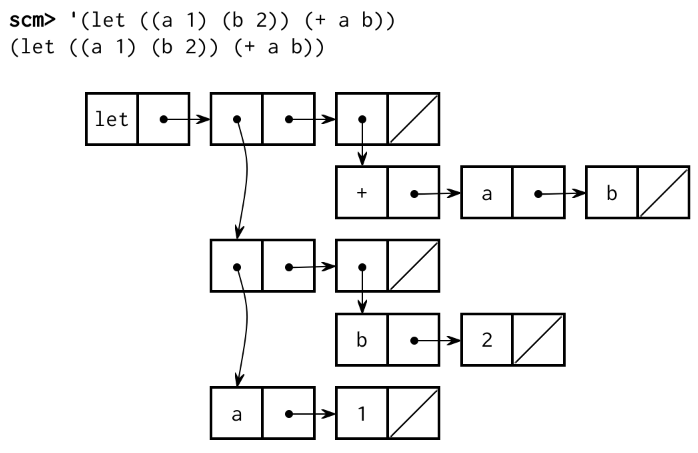 |
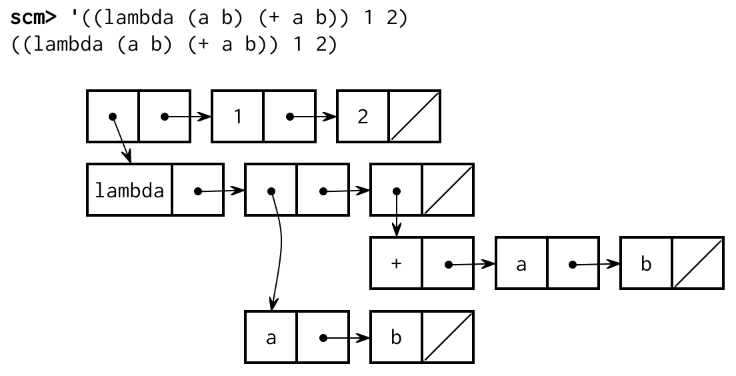 |
Use this rule to implement a procedure called let-to-lambda that rewrites all
let special forms into lambda expressions. If we quote a let expression
and pass it into this procedure, an equivalent lambda expression should be
returned:
scm> (let-to-lambda '(let ((a 1) (b 2)) (+ a b)))
((lambda (a b) (+ a b)) 1 2)
scm> (let-to-lambda '(let ((a 1)) (let ((b a)) b)))
((lambda (a) ((lambda (b) b) a)) 1)
scm> (let-to-lambda 1)
1
scm> (let-to-lambda 'a)
aIn order to handle all programs, let-to-lambda must be aware of Scheme
syntax. Since Scheme expressions are recursively nested, let-to-lambda must
also be recursive. In fact, the structure of let-to-lambda is somewhat
similar to that of scheme_eval--but in Scheme! As a reminder, atoms include
numbers, booleans, nil, and symbols. You do not need to consider code that
contains quasiquotation for this problem.
(define (let-to-lambda expr)
(cond ((atom? expr) <rewrite atoms>)
((quoted? expr) <rewrite quoted expressions>)
((lambda? expr) <rewrite lambda expressions>)
((define? expr) <rewrite define expressions>)
((let? expr) <rewrite let expressions>)
(else <rewrite other expressions>)))map to convert let forms
in every element of a list to the equivalent lambda form.
scm> (zip '((1 2) (3 4) (5 6)))
((1 3 5) (2 4 6))
scm> (zip '((1 2)))
((1) (2))
scm> (zip '())
(() ())Hint 2: In this problem, it may be helpful to build a scheme list that evaluates to a special form
(for instance, a lambda expression). As a related example, the following code builds a scheme list that evaluates to the expression (define (f x) (+ x 1)):
(let ((name-and-params '(f x))
(body '(+ x 1)))
(cons 'define
(cons name-and-params (cons body nil))))Test your implementation by running
Use Ok to test your code:
python3 ok -q optional_1We used
letwhile defininglet-to-lambda. What if we want to runlet-to-lambdaon an interpreter that does not recognizelet? We can passlet-to-lambdato itself to rewrite itself into an equivalent program withoutlet:;; The let-to-lambda procedure (define (let-to-lambda expr) ...) ;; A list representing the let-to-lambda procedure (define let-to-lambda-code '(define (let-to-lambda expr) ...)) ;; A let-to-lambda procedure that does not use 'let'! (define let-to-lambda-without-let (let-to-lambda let-to-lambda-code))
Optional Problem 2 (0 pt)
Macros allow the language itself to be extended by the user. Simple macros can
be provided with the define-macro special form. This must be used like a
procedure definition, and it creates a procedure just like define. However,
this procedure has a special evaluation rule: it is applied to its arguments
without first evaluating them. Then the result of this application is
evaluated.
This final evaluation step takes place in the caller's frame, as if the return value from the macro was literally pasted into the code in place of the macro.
Here is a simple example:
scm> (define (map f lst) (if (null? lst) nil (cons (f (car lst)) (map f (cdr lst)))))
scm> (define-macro (for formal iterable body)
.... (list 'map (list 'lambda (list formal) body) iterable))
scm> (for i '(1 2 3)
.... (print (* i i)))
1
4
9
(None None None)The code above defines a macro for that acts as a map except that it doesn't
need a lambda around the body.
In order to implement define-macro, complete the implementation for
do_define_macro, which should create a MacroProcedure and bind it to the
given name as in do_define_form. Then, update scheme_eval so that calls to
macro procedures are evaluated correctly.
Use Ok to test your code:
python3 ok -q optional_2Conclusion
Congratulations! You have just implemented an interpreter for an entire language! If you enjoyed this project and want to extend it further, you may be interested in looking at more advanced features, like let* and letrec, unquote splicing, error tracing, and continuations.
Submit to Ok to complete the project.
python3 ok --submitIf you have a partner, make sure to add them to the submission on okpy.org.