Introduction

In the next part of the course, we will be working with the Scheme programming language. In addition to learning how to write Scheme programs, we will eventually write a Scheme interpreter in Project 4!

Scheme is a famous functional programming language from the 1970s. It is a dialect of Lisp (which stands for LISt Processing). The first observation most people make is the unique syntax, which uses a prefix notation and (often many) nested parentheses (see http://xkcd.com/297/). Scheme features first-class functions and optimized tail-recursion, which were relatively new features at the time.

Primitives and Defining Variables

Scheme has a set of atomic primitive expressions. Atomic means that these expressions cannot be divided up.

scm> 123
123
scm> #t
True
scm> #f
False

Unlike in Python, the only primitive in Scheme that is a false value is #f and its equivalents, false and False. This means that 0 is not false.

In Scheme, we can use the define special form to bind values to symbols, which we can then use as variables. When a symbol is defined this way, the define special form returns the symbol.

• (define <variable name> <value>)

Evaluates <value> and binds the value to <variable name> in the current environment.

WWSD

scm> (define a 1)

scm> a

scm> (define b a)

scm> b

scm> (define c 'a)

scm> c

Call Expressions

Call expressions apply a procedure to some arguments.

(<operator> <operand1> <operand2> ...)

Call expressions in Scheme work exactly like they do in Python. To evaluate them:

1. Evaluate the operator to get a procedure.
2. Evaluate each of the operands from left to right.
3. Apply the value of the operator to the evaluated operands.

For example, consider the call expression (+ 1 2). First, we evaluate the symbol + to get the built-in addition procedure. Then we evaluate the two operands 1 and 2 to get their corresponding atomic values. Finally, we apply the addition procedure to the values 1 and 2 to get the return value 3.

Operators may be symbols, such as + and *, or more complex expressions, as long as they evaluate to procedure values.

Here is a reference for the Scheme Built-In Procedures.

scm> (- 1 1)                 ; 1 - 1
0
scm> (* (+ 1 2) (+ 1 2))     ; (1 + 2) * (1 + 2)
9

WWSD

What would Scheme display? As a reminder, the built-in quotient function performs floor division.

scm> (define a (+ 1 2))

scm> a

scm> (define b (- (+ (* 3 3) 2) 1))

scm> (+ a b)

scm> (= (modulo b a) (quotient 5 3))

Special Forms

Special form expressions contain a special form as the operator. Special form expressions do not follow the same rules of evaluation as call expressions. Each special form has its own rules of evaluation -- that's what makes them special! Here's the Scheme Specification to reference the special forms we will cover in this class.

If Expression

An if expression looks like this:

(if <predicate> <if-true> [if-false])

<predicate> and <if-true> are required expressions and [if-false] is optional.

The rules for evaluation are as follows:

1. Evaluate <predicate>.
2. If <predicate> evaluates to a truth-y value, evaluate <if-true> and return its value. Otherwise, evaluate [if-false] if provided and return its value.

if is a special form as not all of its operands will be evaluated. The value of the first operand determines whether the second or the third operator is evaluated.

Important: Only #f is a false-y value in Scheme; everything else is truth-y, including 0.

scm> (if (< 4 5) 1 2)
1
scm> (if #f (/ 1 0) 42)
42

Boolean operators

Like Python, Scheme has the boolean operators and, or, and not. and and or are special forms because they are short-circuiting operators, while not is a builtin procedure.

• and takes in any amount of operands and evaluates these operands from left to right until one evaluates to a false-y value. It returns that first false-y value or the value of the last expression if there are no false-y values.
• or also evaluates any number of operands from left to right until one evaluates to a truth-y value. It returns that first truth-y value or the value of the last expression if there are no truth-y values.
• not takes in a single operand, evaluates it, and returns its opposite truthiness value.

scm> (and 25 32)
32
scm> (or 1 (/ 1 0))    ; Short-circuits
1
scm> (not (odd? 10))
#t

WWSD

What would Scheme display?

scm> (if (or #t (/ 1 0)) 1 (/ 1 0))

scm> ((if (< 4 3) + -) 4 100)

Defining Functions

All Scheme procedures are constructed as lambda procedures.

One way to create a procedure is to use the lambda special form.

(lambda (<param1> <param2> ...) <body>)

This expression creates a lambda function with the given parameters and body, but does not evaluate the body. As in Python, the body is not evaluated until the function is called and applied to some argument values. The fact that neither the parameters nor the body is evaluated is what makes lambda a special form.

We can also assign the value of an expression to a name with a define special form:

1. (define (<name> <param> ...) <body> ...)
2. (define <name> (lambda (<param> ...) <body> ...))

These two expressions are equivalent; the first is a concise version of the second.

scm> ; Bind lambda function to square
scm> (define square (lambda (x) (* x x)))
square
scm> (define (square x) (* x x))          ; Same as above
square
scm> square
(lambda (x) (* x x))
scm> (square 4)
16

Q1: Virahanka-Fibonacci

Write a function that returns the n-th Virahanka-Fibonacci number.

(define (vir-fib n)
    (if (<= n 1)
        n
        (+ (vir-fib (- n 1)) (vir-fib (- n 2))))
)

(expect (vir-fib 10) 55)
(expect (vir-fib 1) 1)

scm> (vir-fib 0)
0
scm> (vir-fib 1)
1
scm> (vir-fib 10)
55

Pairs and Lists

All lists in Scheme are linked lists. Scheme lists are composed of two element pairs. We define a list as being either

• the empty list, nil
• a pair whose second element is a list

As in Python, linked lists are recursive data structures. The base case is the empty list.

We use the following procedures to construct and select from lists:

• (cons first rest) constructs a list with the given first element and rest of the list. For now, if rest is not a pair or nil it will error.
• (car lst) gets the first item of the list
• (cdr lst) gets the rest of the list

To visualize Scheme lists, you can use the draw function in code.cs61a.org.

scm> nil
()
scm> (define lst (cons 1 (cons 2 (cons 3 nil))))
lst
scm> lst
(1 2 3)
scm> (car lst)
1
scm> (cdr lst)
(2 3)

Scheme lists are displayed in a similar way to the Link class we defined in Python. Here is an example in 61A Code.

Two other ways of creating lists are using the built-in list procedure or the quote special form. More info can be found on the Scheme Specification.

scm> (list 1 2 3)
(1 2 3)
scm> (quote (1 x 3))
(1 x 3)
scm> '(1 x 3)   ; Equivalent to the previous quote expression
(1 x 3)

=, eq?, equal?

• (= <a> <b>) returns true if a equals b. Both must be numbers.
• (eq? <a> <b>) returns true if a and b are equivalent primitive values. For two objects, eq? returns true if both refer to the same object in memory.
• (equal? <a> <b>) returns true if a and b are equivalent. Two pairs are equivalent if their cars and cdrs are equivalent.

scm> (define a '(1 2 3))
a
scm> (= a a)
Error
scm> (equal? a '(1 2 3))
#t
scm> (eq? a '(1 2 3))
#f

Q2: List Making

Let's make some Scheme lists. We'll define the same list with list, quote, and cons.

The following list was visualized using the draw feature of code.cs61a.org.

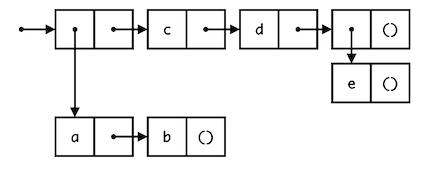
First, use list:

(define with-list
    (list
        (list 'a 'b) 'c 'd (list 'e)
    )
)
(draw with-list)

Now use quote. What differences are there?

(define with-quote
    '(
        (a b) c d (e)
    )

)
(draw with-quote)

Now try with cons. For convenience, we've defined a helpful-list and another-helpful-list:

(define helpful-list
   (cons 'a (cons 'b nil)))
(draw helpful-list)

(define another-helpful-list
    (cons 'c (cons 'd (cons (cons 'e nil) nil))))
(draw another-helpful-list)

(define with-cons
    (cons
        (cons 'a (cons 'b nil)) (cons 'c (cons 'd (cons (cons 'e nil) nil)))
    )
)
(draw with-cons)

Q3: List Concatenation

Write a function which takes two lists and concatenates them.

Notice that simply calling (cons a b) would not work because it will create a deep list. Do not call the builtin procedure append, since it does the same thing as list-concat should do.

(define (list-concat a b)
    (if (null? a)
    b
    (cons (car a) (list-concat (cdr a) b)))
)

(expect (list-concat '(1 2 3) '(2 3 4)) (1 2 3 2 3 4))
(expect (list-concat '(3) '(2 1 0)) (3 2 1 0))

scm> (list-concat '(1 2 3) '(2 3 4))
(1 2 3 2 3 4)

Q4: Map

Write a function that takes a procedure and applies it to every element in a given list using your own implementation without using the built-in map function.

(define (map-fn fn lst)
    (if (null? lst)
        nil
        (cons (fn (car lst)) (map-fn fn (cdr lst))))
)

(map-fn (lambda (x) (* x x)) '(1 2 3))
; expect (1 4 9)

scm> (map-fn (lambda (x) (* x x)) '(1 2 3))
(1 4 9)

Q5: Remove

Implement a procedure remove that takes in a list and returns a new list with all instances of item removed from lst. You may assume the list will only consist of numbers and will not have nested lists.

Hint: You might find the built-in filter procedure useful (though it is definitely possible to complete this question without it).

You can find information about how to use filter in the 61A Scheme builtin specification!

(define (remove item lst)
  (cond ((null? lst) '())
        ((equal? item (car lst)) (remove item (cdr lst)))
        (else (cons (car lst) (remove item (cdr lst)))))
)

(expect (remove 3 nil) ())
(expect (remove 2 '(1 3 2)) (1 3))
(expect (remove 1 '(1 3 2)) (3 2))
(expect (remove 42 '(1 3 2)) (1 3 2))
(expect (remove 3 '(1 3 3 7)) (1 7))

(define (remove item lst)
  (filter (lambda (x) (not (= x item))) lst))