Tree Recursion

A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.

For example, let's say we want to recursively calculate the nth Virahanka-Fibonacci number, defined as:

def virfib(n):
    if n == 0 or n == 1:
        return n
    return virfib(n - 1) + virfib(n - 2)

Calling virfib(6) results in the following call structure that looks like an upside-down tree (where f is virfib):

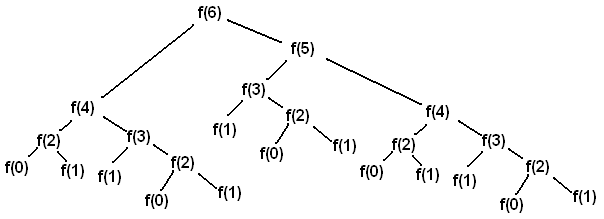
Each f(i) node represents a recursive call to virfib. Each recursive call f(i) makes another two recursive calls, which are to f(i-1) and f(i-2). Whenever we reach a f(0) or f(1) node, we can directly return 0 or 1 rather than making more recursive calls, since these are our base cases.

In other words, base cases have the information needed to return an answer directly, without depending upon results from other recursive calls. Once we've reached a base case, we can then begin returning back from the recursive calls that led us to the base case in the first place.

Generally, tree recursion can be effective for problems where there are multiple possibilities or choices at a current state. In these types of problems, you make a recursive call for each choice or for a group of choices.

Q1: Count Stair Ways

Imagine that you want to go up a flight of stairs that has n steps, where n is a positive integer. You can either take 1 or 2 steps each time. How many different ways can you go up this flight of stairs? In this question, you'll write a function count_stair_ways that solves this problem. Before you code your approach, consider these questions.

How many different ways are there to go up a flight of stairs with n = 1 step? How about n = 2 steps? Try writing out some other examples and see if you notice any patterns.

What’s the base case for this question? What is the simplest input?

What do count_stair_ways(n - 1) and count_stair_ways(n - 2) represent?

Fill in the code for count_stair_ways:

def count_stair_ways(n):
    """Returns the number of ways to climb up a flight of
    n stairs, moving either 1 step or 2 steps at a time.
    >>> count_stair_ways(4)
    5
    """
    if n == 1:
        return 1
    elif n == 2:
        return 2
    return count_stair_ways(n-1) + count_stair_ways(n-2)

def count_stair_ways_alt(n):
    """Returns the number of ways to climb up a flight of
    n stairs, moving either 1 step or 2 steps at a time.
    >>> count_stair_ways_alt(4)
    5
    """
    if n == 0:
        return 1
    elif n < 0:
        return 0
    return count_stair_ways_alt(n-1) + count_stair_ways_alt(n-2)

Q2: Count K

Consider a special version of the count_stair_ways problem, where instead of taking 1 or 2 steps, we are able to take up to and including k steps at a time. Write a function count_k that figures out the number of paths for this scenario. Assume n and k are positive.

def count_k(n, k):
    """ Counts the number of paths up a flight of n stairs
    when taking up to and including k steps at a time.
    >>> count_k(3, 3) # 3, 2 + 1, 1 + 2, 1 + 1 + 1
    4
    >>> count_k(4, 4)
    8
    >>> count_k(10, 3)
    274
    >>> count_k(300, 1) # Only one step at a time
    1
    """
    if n == 0:
        return 1
    elif n < 0:
        return 0
    else:
        total = 0
        i = 1
        while i <= k:
            total += count_k(n - i, k)
            i += 1
        return total

Lists

A list is a data structure that can store multiple elements. Each element can be any type, even a list itself. We write a list as a comma-separated list of expressions in square brackets:

>>> list_of_ints = [1, 2, 3, 4]
>>> list_of_bools = [True, True, False, False]
>>> nested_lists = [1, [2, 3], [4, [5]]]

Each element in the list has an index, with the index of the first element starting at 0. We say that lists are therefore "zero-indexed."

With list indexing, we can specify the index of the element we want to retrive. A negative index represents starting from the end of the list, so the negative index -i is equivalent to the positive index len(lst)-i.

>>> lst = [6, 5, 4, 3, 2, 1, 0]
>>> lst[0]
6
>>> lst[3]
3
>>> lst[-1] # Same as lst[6]
0

List slicing

To create a copy of part or all of a list, we can use list slicing. The syntax to slice a list lst is: lst[<start index>:<end index>:<step size>].

This expression evaluates to a new list containing the elements of lst:

• Starting at and including the element at <start index>.
• Up to but not including the element at <end index>.
• With <step size> as the difference between indices of elements to include.

If the start, end, or step size are not explicitly specified, Python has default values for them. A negative step size indicates that we are stepping backwards through a list when including elements.

>>> lst[:3]   # Start index defaults to 0
[6, 5, 4]
>>> lst[3:]   # End index defaults to len(lst)
[3, 2, 1, 0]
>>> lst[::-1]   # Make a reversed copy of the entire list
[0, 1, 2, 3, 4, 5, 6]
>>> lst[::2]  # Skip every other; step size defaults to 1 otherwise
[6, 4, 2, 0]

List comprehensions

List comprehensions are a compact and powerful way of creating new lists out of sequences. The general syntax for a list comprehension is the following:

[<expression> for <element> in <sequence> if <conditional>]

where the if <conditional> section is optional.

The syntax is designed to read like English: "Compute the expression for each element in the sequence (if the conditional is true for that element)."

>>> [i**2 for i in [1, 2, 3, 4] if i % 2 == 0]
[4, 16]

This list comprehension will:

• Compute the expression i**2
• For each element i in the sequence [1, 2, 3, 4]
• Where i % 2 == 0 (i is an even number),

and then put the resulting values of the expressions into a new list.

In other words, this list comprehension will create a new list that contains the square of every even element of the original list [1, 2, 3, 4].

We can also rewrite a list comprehension as an equivalent for statement, such as for the example above:

>>> lst = []
>>> for i in [1, 2, 3, 4]:
...     if i % 2 == 0:
...         lst = lst + [i**2]
>>> lst
[4, 16]

Q3: WWPD: Lists

What would Python display?

>>> a = [1, 5, 4, [2, 3], 3]
>>> print(a[0], a[-1])

>>>len(a)

>>> 2 in a

>>> a[3][0]

Q4: Even weighted

Write a function that takes a list s and returns a new list that keeps only the even-indexed elements of s and multiplies them by their corresponding index.

def even_weighted(s):
    """
    >>> x = [1, 2, 3, 4, 5, 6]
    >>> even_weighted(x)
    [0, 6, 20]
    """
    return [i * s[i] for i in range(len(s)) if i % 2 == 0]

result = []
for i in range(len(s)):
    if i % 2 == 0:
        result = result + [i * s[i]]
return result

Q5: Max Product

Write a function that takes in a list and returns the maximum product that can be formed using nonconsecutive elements of the list. The input list will contain only numbers greater than or equal to 1.

def max_product(s):
    """Return the maximum product that can be formed using
    non-consecutive elements of s.
    >>> max_product([10,3,1,9,2]) # 10 * 9
    90
    >>> max_product([5,10,5,10,5]) # 5 * 5 * 5
    125
    >>> max_product([])
    1
    """
    if s == []:
        return 1
    else:
        return max(max_product(s[1:]), s[0] * max_product(s[2:]))